Retvinklet trekant
Retvinklet trekant
I dette afsnit vil vi mest beskæftige os med trekanter og deres egenskaber.
En trekant afgrænses af 3 linjestykker. Linjernes skæringspunkter kalder man for vinkelspidser og betegnes ofte med bogstaverne $latex A$, $latex B$ og $latex C$. Linjestykkerne som forbinder vinkelspidserne, kaldes for trekantens sider eller kateter. Vinkelsummen i enhver trekant er på 180 grader.
En trekant kaldes for en retvinklet trekant, hvis den indeholder en vinkel på præcis 90 grader og stumpvinklet, hvis en af vinklerne er over 90 grader.
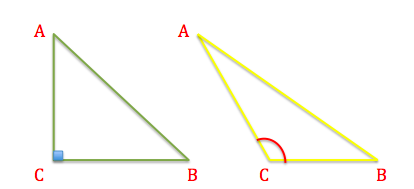
Den grønne trekant er retvinklet, firkanten i vinkel $latex C$ angiver at vinklen er ret. I den gule trekant ses at vinkel $latex C$ er stump. Vinkel $latex C$'s modstående side, kaldes ofte for hypotenusen. Den længste side i en trekant kaldes altid for hypotenusen.
Areal for en retvinklet trekant
En retvinklet trekant har arealet:
$latex T=\frac{1}{2}ab$
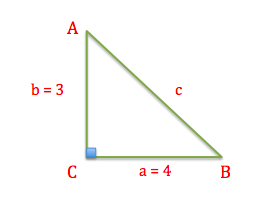
Tager vi udgangspunkt i den grønne trekant foroven, kan vi altså beregne dens areal ved at gange 1/2 med grundfladen $latex a$ og højden $latex b$. Dvs.
$latex T=\frac{1}{2}ab=\frac{1}{2}\cdot4\cdot3=6$
Arealet af ovenstående trekant er altså 6.
Pythagoras læresætning
Pythagoras sætning angår forholdet mellem længden af siderne i en retvinklet trekant. Den lyder: Summen af kateternes kvadrater, i en retvinklet trekant, er lig med kvadratet på hypotenusen. I symbolsk notation:
$latex a^2+b^2=c^2$
Bevis
[video width="768" height="576" mp4="https://matlet.dk/wp-content/uploads/matlet.dk/2013/10/pythagoras-stning.mp4"][/video]
Vi kan nu med udgangspunkt i Pythagoras læresætning beregne hypotenusen $latex c$ i den retvinklede grønne trekant.
Vi tager udgangspunkt i formlen og indsætter de kendte værdier.
$latex a^2+b^2=c^2\leftrightarrow \sqrt{a^2+b^2}=c$
$latex 4^2+3^2=c^2\leftrightarrow\sqrt{4^2+3^2}=5$
Vi ser altså at hypotenusen er 5 i den grønne retvinklede trekant.
