Punkter og vektorer

Vi skal her forbinde punkter i et koordinatsystem med vektorer.

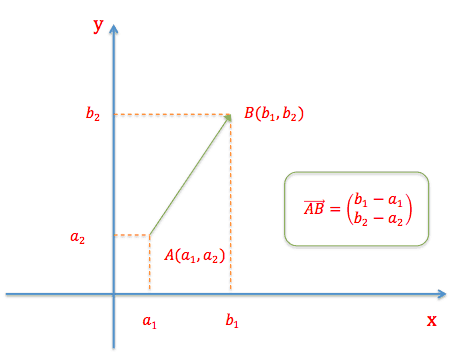
Figuren her viser altså en vektor, der er fastlagt ved de 2 punkter \(A\) og \(B\).

\(\vec{AB}=\begin{pmatrix} b_1-a_1 \\ b_2-a_2 \end{pmatrix}\)

Vektorens koordinater bestemmes ved at trække \(A\)’s koordinater fra \(B\)’s. Vi kan også bestemme afstanden mellem de 2 punkter \(A\) og \(B\). Afstanden 2 punkter er nemlig lig med længden af vektoren, der forbinder punkterne. Dvs.

\(|AB|=\sqrt{(b_1-a_1)^2+(b_2-a_2)^2}\)

Afstandsformlen

Afstanden mellem 2 punkter \(A(a_1,a_2)\) og \(B(b_1,b_2)\) findes ved:

\(|AB|=\sqrt{(b_1-a_1)^2+(b_2-a_2)^2}\)

Ved hjælp af formlen kan vi altså beregne afstanden mellem 2 punkter i et koordinatsystem eller længden af en vektor. Lad os tage et eksempel.

Vi ønsker at bestemme afstanden mellem \(A(2,5)\) og \(B(6,9)\) findes ved:

\(|AB|=\sqrt{(6-2)^2+(9-5)^2}\)

\(=\sqrt{16+16}\)

\(=\sqrt{32}\)

Lad os som det næste indtegne en trekant \(ABC\) ind i et koordinatsystem.

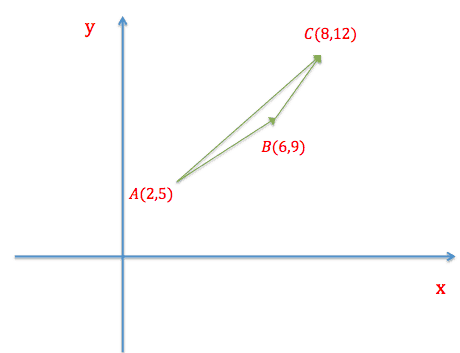
Ud fra vinkelspidsernes koordinater kan vi beregne koordinaterne til de 3 vektorer

\(|AB|=\begin{pmatrix} 6 \\ 9 \end{pmatrix}-\begin{pmatrix} 2 \\ 5 \end{pmatrix}=\begin{pmatrix} 4 \\ 4 \end{pmatrix}\)

\(|BC|=\begin{pmatrix} 8 \\ 12 \end{pmatrix}-\begin{pmatrix} 6 \\ 9 \end{pmatrix}=\begin{pmatrix} 2 \\ 3 \end{pmatrix}\)

\(|AC|=\begin{pmatrix} 8 \\ 12 \end{pmatrix}-\begin{pmatrix} 2 \\ 5 \end{pmatrix}=\begin{pmatrix} 6 \\ 7 \end{pmatrix}\)

Læg nu mærke til, at

\(|AB|+|BC|=|AC|\)

Det ses altså her, at der er præcis sammenhæng mellem geometrien samt beregningerne. Ovennævnte eksempel illustrerer faktisk en vigtig regel indenfor vektorregning kaldet for indskudsreglen.

Indskudsreglen

Der antages her 3 punkter \(A(a_1, a_2)\), \(B(b_1,b_2)\) og \(C(c_1, c_2)\). Der gælder nu:

\(\vec{AB}+\vec{BC}=\vec{AC}\)

Bevis:

\(\begin{pmatrix} b_1-a_1 \\ b_2-a_2 \end{pmatrix}+\begin{pmatrix} c_1-b_1 \\ c_2-b_2 \end{pmatrix}=\begin{pmatrix} c_1-a_1 \\ c_2-a_2 \end{pmatrix}\)

Stedvektor

Ved vektorregning støder man til tider på stedvektorer. En stedvektor har samme koordinater som spidsen på pilen. Lad os kigge på et konkret geometrisk illustration.

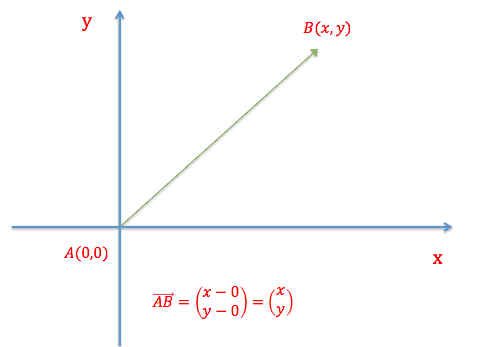
Det ses altså her at stedvektoren har samme koordinat som punktet B.

Opgaver

Beregn vektor a), b) og c)

\(\begin{pmatrix} b_1-a_1 \\ b_2-a_2 \end{pmatrix}\)

a) \(\quad BA\)

b) \(\quad CA\)

c) \(\quad CB\)

Hvor \(A(10,8)\), \(B(3, -4)\) og \(C(-10,9)\).

Løsning

Opgaver                                                                                                                                            

Udregn følgende vektorer:

\(AC=AB+BC\)

\(A(5,3)\)
\(B(7,17)\)
\(C(21,16)\)

Løsning