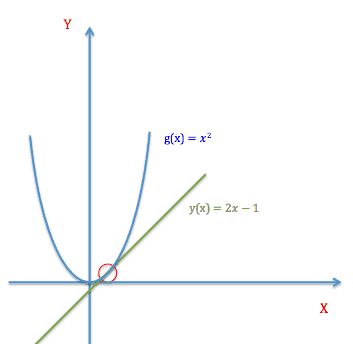
I matematik samt fysik spiller en tangent til eksempelvis en parabel en vigtig rolle. I denne sektion vil vi, givet en funktionsforskrift samt et røringspunkt bestemme ligningen for tangenten til røringspunktet.
Tangentligning
Hvis vi kender en differentiabel funktion \(y=f(x)\) og en \(x\)-værdi, \(x_0\). Da vil tangenten i kurvepunktet, \(x_0\), have ligningen:
\(y-f(x_0)=f'(x_0)(x-x_0)\)
Lad os kigge på et konkret eksempel
Vi ønsker nu at bestemme en ligning for en tangent til grafen \(f\), i røringspunktet \(x=1\). DVS. røringspunktet ved 1, på \(x\)-aksen.
\(f(x)=x^2\)
\(f'(x)=2x\)
\(f'(1)=2\cdot1=2\)
\(f(1)=1^2=1\)
\(y-f(x_0)=f'(x_0)(x-x_0)\rightarrow y-1=2(x-1)\leftrightarrow y=2x-1\)
Opgaver
Udregn tangentens ligning til funktionen \(f(x)\) der løber igennem punktet \(P(2,0)\):
- \(f(x)=x^2-2x+8,\quad\quad\text{pkt. }P(2,0)\)
Se løsningen
Udregn tangentens ligning til funktionen \(f(x)\) der løber igennem punktet \(P(2,14\):
- \(f(x)=x^2+4x+2,\quad\quad\text{pkt. }P(2,14)\)
Se løsningen