Tangent og sekant

Indenfor differentialregning bruges der ofte begreberne tangent og sekant. Derfor vil vi herunder forklare mere om, hvad de to begreber er for noget.

Tangent

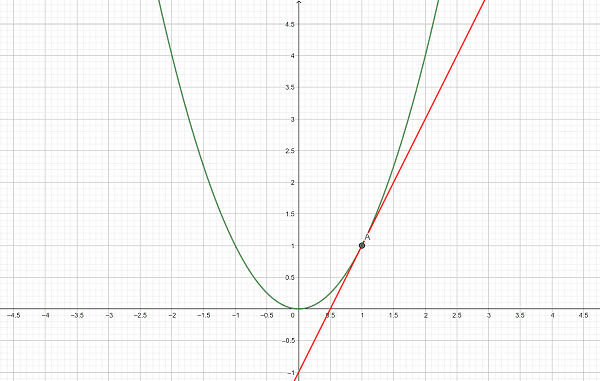
En tangent er en ret linje, som ligger sig op ad funktionsgrafen. En tangent er anvendelig til at sætte et tal på, hvor meget en funktion vokser eller aftager i et givet punkt. I nedenstående figur kan du se et eksempel på en tangent.

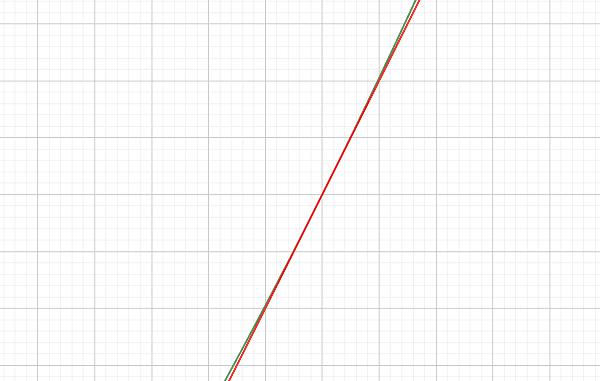
Selvom det kan være svært at se forskel på tangenten og funktionsgrafen, hvis vi zoomer helt tæt på (jf. nedenstående billede), så rører tangenten kun funktionsgrafen i ét punkt.

Da tangenten er en lineær funktion ved vi fra tidligere, at tangenten har forskriften:

\(y=a\cdot x+b\),

hvor \(a\) er hældningen (dvs. hvor meget vi går op eller ned, når vi går 1 hen af \(x\)-aksen) og \(b\) er skæringspunktet med \(y\)-aksen (læg mærke til, at vi skriver \(y\) i stedet for \(f(x)\)). Kender vi funktionsforskriften for grafen, \(f(x)\), og røringspunktet, er det muligt at bestemme tangents ligning. Dette vil vi se nærmere på i næste afsnit.

Sekant

Ved differentialregning er vi interesseret i tangents hældning. Men som du lærte på C-niveau, skal vi kende to punkter for at beregne hældningen for en lineær funktion. Men da vi kun kender et punkt, har vi et problem. Det er her sekanten bliver brugbar.

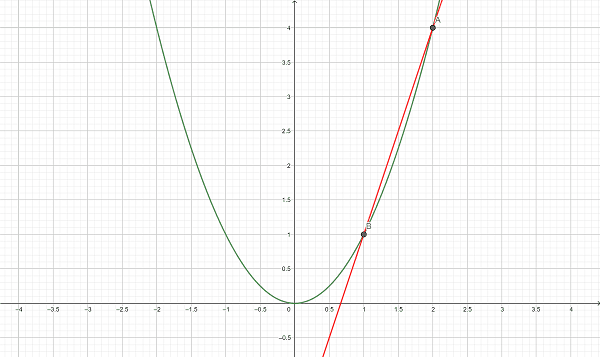
En sekant er en ret linje, som skærer funktionsgrafen i to punkter. Dvs. tilføjer vi andet vilkårligt skæringspunkt til vores første figur (lad os tag punktet \((2,4)\)), skærer vores rette linje nu funktionsgrafen i to punkter (hhv. \(A\) og \(B\) – dvs. den røde linje er sekanten).

Hvordan vi kommer fra sekanten til tangentens hældning, vil vi se nærmere på i en af de næste afsnit.