Vi vil her tage udgangspunkt i vilkårlige trekanter. Det betyder ikke kun retvinklede trekanter, men også stumpvinklede trekanter og spidsvinklede trekanter. Vi starter her med at udlede sinusrelationerne.
Udledning af sinusrelationerne
Vi tager her udgangspunkt i en vilkårlig trekant, hvor højden falder indenfor som vi kan se. Vi går nu i gang med at udlede sinusrelationerne. Tager vi udgangspunkt i følgende vilkårlige trekant \(ABC\), og tegner højden ned fra vinkel \(C\) ned til grundlinjen så deler vi trekant \(ABC\) i to retvinklede trekanter:
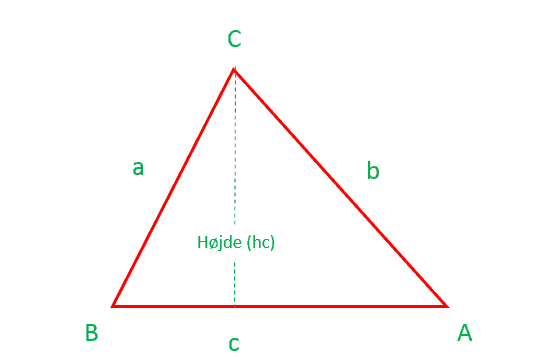
Om retvinklede trekanter gælder der
\(\sin{(V)}=\frac{\text{modstående katete}}{\text{hypotenusen}}\)
Tager vi nu udgangspunkt i en af de to små retvinklede trekanter, eksempelvis trekanten til venstre får vi nu:
\(\sin{(B)}=\frac{hc}{a}\leftrightarrow\sin{B\cdot a}=hc\)
Vi kan også beregne den højre retvinklede trekant:
\(\sin{(A)}=\frac{hc}{b}\leftrightarrow \sin{A\cdot b}=hc\)
Vi kan nu se, at højden åbenbart kan udtrykkes på 2 forskellige måder.
Sætter vi dem nu sammen, får vi
\(\sin{A\cdot b}=\sin{B\cdot a}\)
\(\frac{\sin{A}}{a}=\frac{\sin{B}}{b}\)
Vi har nu udledt vores første sinusrelation. Vi kunne dog også på tilsvarende vis have valgt at trække højden fra \(A\) eller højden fra \(C\), med samme resultat, blot med andre sider og vinkler. Der eksisterer derfor tre sinusrelationer i alt. Disse er givet her:
\(\frac{\sin{A}}{a}=\frac{\sin{B}}{b}=\frac{\sin{C}}{c}\)
Som nævnt falder højden i den “vilkårlige” trekant, inden for trekantens sider. Men med en mindre ændring er det naturligvis også muligt også at udlede sinusrelationen i det konkrete tilfælde, hvor højden falder udenfor.












