Vi har tidligere i den todimensionale verden kunnet beskrive en ret linje ved ligningen \(y=ax+b\), hvor \(b\) er skæringspunktet med den lodrette akse og stigningstallet, \(a\). I den tredimensionale verden benytter man sig af parameterfremstillinger til at beskrive rette linjer i rummet. Vi så tidligere i planen, at for at beskrive en linje kræves der kendskab med et kendt punkt \(P\) samt en retningsvektoren:
\(P=(x_0, y_0, z_0), \quad\quad\vec{r}=\left(\begin{matrix} a_1 \\ a_2 \\ a_3 \end{matrix}\right)\)
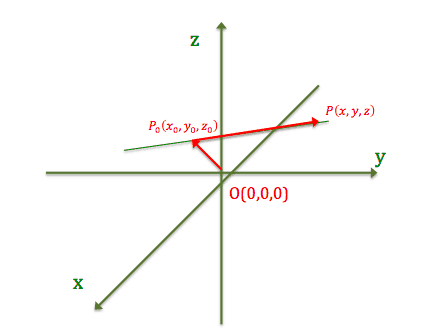
Lad os kaste et blik i koordinatsystemet, hvor vi har en grøn ret linje, et løbende punkt samt det kendte punkt.
Vi kan nu bestemme stedvektoren til det løbende punkt \(P\) ved at anvende indskudsreglen.
\(\vec{OP}=\vec{OP_0}+\vec{P_0P}\)
Sidste led på højresiden er parallel med retningsvektoren, derfor kan det skrives som et tal, \(t\), ganget med retningsvektoren. Det vil sige:
\(\vec{OP}=\vec{OP_0}+\vec{P_0P}\leftrightarrow\vec{OP}=\vec{OP_0}+t\vec{r}\leftrightarrow \left(\begin{matrix} x \\ y \\ z \end{matrix}\right)=\left(\begin{matrix} x_0 \\ y_0 \\ z_0 \end{matrix}\right)+t\cdot \left(\begin{matrix} a_1 \\ a_2 \\ a_3 \end{matrix}\right)\)
Læg her mærke til at parameterfremstillingen ligner den fra planen. Der er her kommet en ekstra række på. Ligesom i planen kan vi også skrive parameterfremstillingen som 3 koordinatligninger.
\(x=x_0+ta_1\)
\(y=y_0+ta_2\)
\(z=z+ta_3\)
Lad os kigge på et konkret eksempel:
Linje gennem to punkter
Der er her givet 2 punkter \(A(1,3,3)\) og \(B(3,-1,2)\). For at bestemme parameterfremstillingen, kræves det at vi bestemmer retningsvektoren, dertil anvendes de 2 punkter.
\(\vec{r}=\vec{AB}=\left(\begin{matrix} 3-1 \\ -1-3 \\ 2-1 \end{matrix}\right)=\left(\begin{matrix} -2 \\ -4 \\ 1 \end{matrix}\right)\)
Som et kendt anvendes punktet \(A\). Herved får vi parameterfremstillingen:
\(\left(\begin{matrix} x \\ y \\ z \end{matrix}\right)=\left(\begin{matrix} 1 \\ 3 \\ 3 \end{matrix}\right)+t\cdot\left(\begin{matrix} -2 \\ -4 \\ 1 \end{matrix}\right)\)
Skæring mellem linjer
Vi har nu set, hvorledes vi bestemmer parameterfremstillingen for en linje. Vi så tidligere i planen at, hvis 2 linjer ikke er parallelle må disse 2 linjer skære hinanden i ét punkt. Næsten samme regler gøres gældende for linjer i rummet:
- Hvis linjerne er parallelle
- Enten vil der være uendelig mange skæringspunkter
- Der vil ingen skæringerpunkter være overhovedet
- Hvis linjerne ikke er parallelle, gælder følgende udsagn
- Linjerne vil skærer hinanden i ét enkelt punkt ELLERS
- Linjerne er vindskæve og kommer aldrig til at skærer hinanden
Opgaver
Det er her givet 2 punkter:
\(A(3,-2,1)\)
\(B(-5,3,-1)\)
- Bestem en parameterfremstilling for linjen gennem \(A\) samt \(B\)
- Undersøg om punktet \(P(-1,\frac{1}{2},1)\) ligger på linjen
Løsning