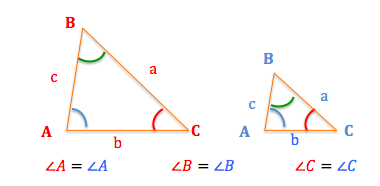
Ensvinklede trekanter har præcis samme vinkler, som vi kan se i ovenstående figur. To sider fra hver deres trekant er dermed ensliggende, hvis de grænser op til vinklerne af samme størrelse. Eksempelvis er siderne \(a\) og \(a\) ensliggende, \(b\) og \(b\) er også ensliggende og det samme er tilfældet for \(c\) og \(c\).
Det specielle ved ensliggende sider i ensvinklede trekanter er, at den ene betragtes som en forstørret udgave af den anden.
Generelt gælder der at forholdene mellem ensliggende sider er lige store, hvis trekanterne er ensvinklede. I dette specielle tilfælde, gælder der:
\(\frac{a}{a}=\frac{b}{b}=\frac{c}{c}\)
Der eksisterer med andre ord et fast forhold mellem ensliggende sider i ensvinklede trekanter. I matematik kaldes dette forhold for enten $K$-tallet, proportionalitetsfaktoren eller skalafaktor – afhængig af din matematikbog. Det betyder dog præcis det samme.
Bevis – ensvinklede trekanter
Eksempel
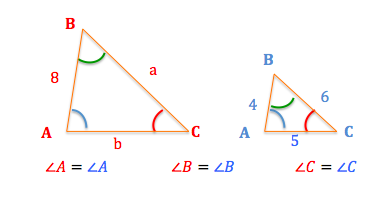
Vi ser her 2 ensvinklede trekanter \(ABC\) samt \(ABC\).
Vi har yderligere fået opgivet en række sider. Vi har blandt andet fået opgivet siderne \(c\) og \(c\) til henholdsvis 8 og 4. Vi kan hermed beregne skalafaktoren, \(k\), til:
\(k=\frac{c}{c}=\frac{8}{4}=2\)
Vi kan nu beregne siderne \(a\) og \(b\).
\(a=k\cdot a=2\cdot 6=12\)
\(b=k\cdot b=2\cdot 5=10\)
Vi har altså nu beregnet siderne \(a\) og \(b\) til henholdsvis 12 og 10.
Opgaver
Udregn følgende ukendte sider i følgende ensvinklede trekanter.
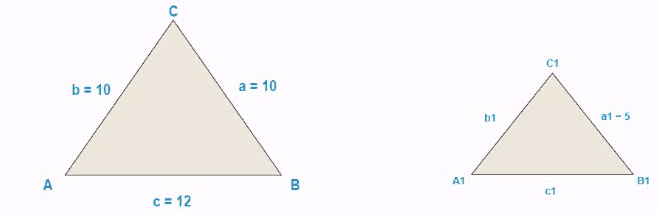
og herefter beregn de ukendte sider i følgende trekant:
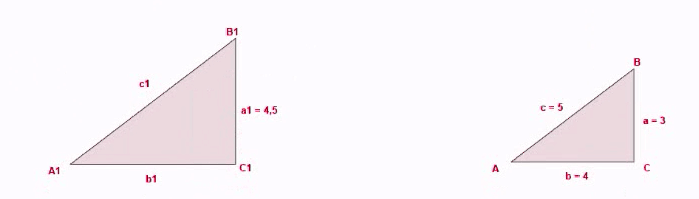
Se løsningerne