I visse tilfælde støder man ind på opgaver, hvor man ikke kan nøjes med at anvende sinusrelationerne til at beregne de ukendte vinkler og sider i en trekant. Her kan man ofte anvende cosinusrelationerne.
Styrken ved cosinusrelationerne er, at de gælder ikke kun i retvinklede trekanter, men i vilkårlige trekanter. Det vil sige at det er underordnet om trekanten er retvinklet eller stumpvinklet. Vi kan anvende cosinusrelationerne til alle trekanter.
Cosinusrelationerne
\(\cos{(A)}=\frac{b^2+c^2-a^2}{2bc}\leftrightarrow a^2=b^2+c^2-2bc\cdot\cos{(A)}\)
\(\cos{(B)}=\frac{a^2+c^2-b^2}{2ac}\leftrightarrow b^2=a^2+c^2-2ac\cdot\cos{(B)}\)
\(\cos{(C)}=\frac{a^2+b^2-c^2}{2ab}\leftrightarrow c^2=a^2+b^2-2ab\cdot\cos{(C)}\)
Vi kan altså anvende cosinusrelationerne til at beregne en side i en vilkårlig trekant, i tilfælde af at man kender 2 sider og netop den vinkel, der er imellem siderne.
Bevis – cosinusrelationerne
Eksempel
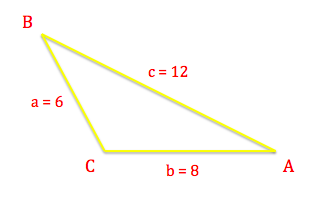
Vi ser her en vilkårlig trekant \(ABC\), hvor \(a=6\), \(b=8\) og \(c=12\). Vi ønsker nu at beregne samtlige vinkler i trekanten ved hjælp af cosinusrelationerne. Vi begynder her, at beregne \(\cos{(A)}\):
\(\cos{(A)}=\frac{b^2+c^2-a^2}{2bc}\rightarrow\cos{(A)}=\frac{8^2+12^2-6^2}{2\cdot8\cdot12}=0,896\)
Vi har nu beregnet \(\cos{(A)}\) til 0,896. Vi beregner vinkel \(A\) ved at sige:
\(\cos^{-1}(0,896)=26,4°\)
Vi finder vinkel \(A\) til 26,4 grader. På samme vis kan vi nu beregne vinkel \(B\):
\(\cos{(B)}=\frac{a^2+c^2-b^2}{2ac}\rightarrow\cos{(B)}=\frac{6^2+12^2-8^2}{2\cdot6\cdot12}=0,806\)
\(\angle B=\cos^{-1}{(0,806)}=36,4°\)
Vi kan nu nemt bestemme den sidste vinkel ved at fratrække vinkel \(B\) og \(A\) fra 180 grader:
\(\angle C=180°-36,4°-26,4°=117,2°\)
Opgaver
Udregn samtlige vinkler og sider, når vi kender:
\(\angle B=85°,\quad a=5,\quad c=9\)
Se løsningen
Udregn samtlige vinkler og sider, når vi kender:
\(\angle B=50°,\quad a=16,\quad c=10\)
Se løsningen
Udregn samtlige vinkler og sider, når vi kender:
\(\angle A=65°,\quad \angle B=85°,\quad c=6\)
Se løsningen