For at beregne arealet A(x) mellem den vandrette akse samt en funktion \(f(x)\), skal vi anvende integration.
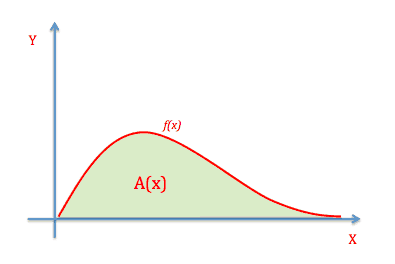
Ved integration beregnes med andre ord det grønne område under grafen og den vandrette akse. Arealet er en funktion af x, det vil sige arealet vokser i x. Jo større område funktion dækker på x-aksen, des større bliver det grønne område og dermed også arealet. I alle tilfælder ønsker man at beregne arealet mellem den vandrette akse og funktionen \(f(x)\) i et afgrænset interval. I matematik på B – niveau, beregner man normalt arealet for den del af funktionen \(f\), der ligger over den vandrette akse, dvs. for \(f(x)>0\).
Det bestemte integral
Vi har nedenunder afgrænset et interval på x-aksen, som vi vil beregne arealet for.
I dette tilfælde kan vi beregne det grønne areal, der løber fra \(a\) til \(b\) på den vandrette akse (x-aksen) og vandrette akse og funktionen \(f(x)\) på den den lodrette akse (y-aksen) ved følgende formel.
Hvis \(f(x)>0\) er kontinuert i intervallet \([a; b]\) med stamfunktionen \(F\). Da beregnes arealet mellem \(f\) og den vandrette akse ved:
\(F(b)-F(a)\)
\(A=\int_a^b f(x)\,\text{d}x=[F(x)]^b_a=F(b)-F(a)\)
Vi integrerer altså med andre ord funktionen \(f(x)\) over intervallet \([a; b]\) for at beregne arealet mellem funktionen og grafen for \(f(x)\). De 2 tal, \(a\) og \(b\) bliver kaldt for integrationsgrænserne, det vil sige at vi integrerer mellem \(a\) og \(b\) på den vandrette akse. Siden vi integrerer mellem et bestemt interval på x-aksen, kalder vi integralet for det bestemte integral. Ovenstående sætning er sand for \(f(x)>0\).
Bevis
I tilfælde af, at \(f(x)<0\), vil grafen for denne samt den vandrette akse stadig danne et areal. I disse tilfælde kan vi naturligvis også beregne arealet mellem grafen og den vandrette akse.
Hvis \(f(x)<0\) er kontinuert i intervallet \([a; b]\) med stamfunktionen \(F\). Da beregnes arealet mellem \(f\) og den vandrette akse ved:
\(F(a)-F(b)\)
\(A=-\int_a^b f(x)\,\text{d}x=-[F(x)]^b_a=F(a)-F(b)\)
Da vi beregner et areal giver det bestemte integral et tal, hvorimod det ubestemte integral giver en stamfunktion.
\(\int_a^b f(x)\,\text{d}x=\text{et tal}\)
\(\int f(x)\,\text{d}x=\text{en funktion}\)
Lad os se et taleksempel om, hvorledes vi udregner et bestemt integral og dermed beregne arealet af en funktion \(f(x)\).
Eksempel
lad os tage udgangspunkt i følgende funktion
\(f(x)=x^2+2\)
Vi ønsker nu at beregne arealet af området under grafen for \(f(x)\) og den vandrette akse fra 1 til 3. Ifølge vores teori må arealet være lig med integralet af funktionen fra 1 til 3.
\(A=\int_1^3 x^2+1\,\text{d}x=\left[\frac{1}{3}x^3+x\right]^3_1=\frac{1}{3}3^3+3-\left(\frac{1}{3}3^1+1\right)=12-2=10\)
Vi får altså et areal på 10, vi starter altså med at tage udgangspunkt i vores funktion \(f(x)\), herefter bestemmer vi det ubestemte integral, hvorefter vi tager integrationsgrænserne i betragtning.
Prøv nu at teste dig selv ved at løse
\(\int^3_1 x^2+2x\,\text{d} x\)
Se løsningen
Indskudsreglen
Hvis vi antager at funktionen \(f(x)\) er kontinuert i intervallet \(I\), da kan intergrationen foretages særskilt i hvert interval. Da gælder der for tallene \(a\), \(b\) og \(c\).
\(\int_a^b f(x)\,\text{d}x=\int_a^c f(x)\,\text{d}x+\int^b_c f(x)\,\text{d}x\)
Bevis
\(\int_a^c f(x)\,\text{d}x+\int_c^b f(x)\,\text{d}x=[F(x)]^c_a+[F(x)]^b_c\)
\(=F(c)-F(a)+F(b)-F(c)\)
\(=F(b)-F(a)\)
\(=\int_a^b f(x)\,\text{d}x\)
Regneregler
Vi vil opsummere de vigtigste regneregler indenfor integration herunder. Vi antager, at \(f\) er en kontinuerlig funktion i et interval, der indeholder konstanterne \(a\), \(b\) og \(c\).
\(\int_a^c f(x)\,\text{d}x+\int_c^b f(x)\,\text{d}x=\int_a^b f(x)\,\text{d}x\)
\(\int_a^a f(x)\,\text{d}x=0\)
\(\int_a^b c\cdot f(x)\,\text{d}x=c\cdot \int_a^b f(x)\,\text{d}x\)
\(\int_a^b f(x)\,\text{d}x=-\int_b^a f(x)\,\text{d}x\)
Opgaver
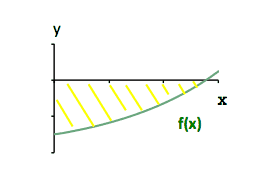
1. Beregn her arealet af det gule skraverede område, når vi får at vide at \(f(x)\) har følgende forskrift
\(f(x)=e^{\frac{x}{2}}-4\)
2. Diskuter kort om arealet for det skraverede område fundet, er rimelig?
Se løsningen
Udregn følgende integraler
a) \(f_1(x)=e^{2x}, \quad\quad\quad a=2, \quad b=4\)
b) \(f_2(x)=x-x^3-x^5, \quad a=-2, \quad b=2\)
Se løsningen
Udregn følgende integraler
a) \(f_1(x)=\int_0^2(x+8^2+2)\,\text{d}x\)
b) \(f_2(x)=\int_1^3\left(\frac{1}{x}+2x^{-1}\right)\,\text{d}x\)
Se løsningen
Udregn følgende integral
a) \(b(t)=\frac{1}{k}(1-e^{-kt}), \quad\quad k=2, \quad a=0, \quad b=2\)
Se løsningen













