Arealformlen

Vi kan anvende sinusrelationerne til at bestemme arealet for en trekant. Sinusrelationerne er nemlig beslægtede med formlen for en trekants areal.

\(T=\frac{1}{2}\cdot\text{højde}\cdot\text{grundlinje}\)

Hvis vi nu husker tilbage på sinusrelationen: I en retvinklet trekant \(ABC\) gælder:

\(\sin{A}=\frac{a}{c}=\frac{\text{modstående katete}}{\text{hypotenusen}}\)

Dette svarer i vores tilfælde til:

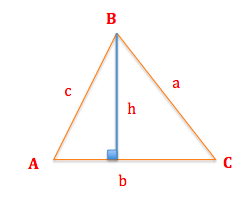
\(h=c\cdot\sin{(A)}\)

Udnytter vi dette udtryk og indsætter det på højdens plads i formlen for arealet af trekantsarealet, får vi:

\(T=\frac{1}{2}\cdot\text{højde}\cdot\text{grundlinje}=\frac{1}{2}\cdot h\cdot b=\frac{1}{2}\cdot a\cdot\sin{(A)}\cdot b\)

Vi har altså hermed udregnet arealet for trekanten ud fra siderne \(b\) og \(c\) samt vinkel \(A\). På tilsvarende vis med udgangspunkt i de 2 andre vinkler kan vi også beregne arealet for trekant \(ABC\).

Vi kan altså konkludere at arealet \(T\) af en trekant \(ABC\) kan beregnes ved hjælp af følgende formler:

\(T=\frac{1}{2}\cdot a\cdot b\cdot\sin{(C)},\quad T=\frac{1}{2}\cdot a\cdot c\cdot\sin{(B)},\quad T=\frac{1}{2}\cdot a\cdot b\cdot\sin{(A)}\)

Vi vil nu udføre en række udledninger for ovenstående resultat, med udgangspunkt i 2 forskellige vinkler i stumpvinklede trekanter samt en spidsvinklet trekant. Vi starter med bevise de ovenstående resultater, når højden \(h\) falder udenfor trekanten og til sidst når den falder i selve trekanten.

Bevis, 1 – Stumpvinklet

Bevis, 2 – Stumpvinklet

Vi skal herunder bevise ovenstående resultat, når højden \(h\) kan måles indefra selve den vilkårlige trekant.

Bevis, 3 – Spidsvinklet

Opgaver                                                                                                                                            

Udregn arealet for en trekant \(ABC\), når:

1. \(\quad\angle A=50°,\quad b=9,\quad c=10\)
2. \(\quad\angle C=55°,\quad a=14,\quad b=7\)

Se løsningerne