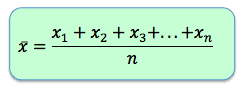I både statslige og videnskabelige undersøgelser arbejder man ofte med meget store datamaterialer i mange forskellige sammenhænge. Staten kan eksempelvis være interesseret i at vide om en specifik motorvej skal udvides med nye baner, for at reducere trafikprop. I dette tilfælde starter man med at skaffe sig et overblik over, hvor befærdet vejen er ved hjælp af deskriptiv statistik, for at vurdere om det kan betale sig at bruge statsmidler til at udvide motorvejen.
Ugrupperede observationer
Vi skal her i denne sektion stifte bekendtskab med nogle redskaber til systematisering og beskrivelse af datasæt. Vi begynder her med et eksempel fra skoleverdenen. I klassen 1. g, på en handelsskole går der 30 elever, hvoraf de 13 er drenge. Vi er i denne undersøgelse interesseret i at føre statistik over drengenes højde i klassen.
Tabellen kaldes for et observationssæt. Til at beskrive observationssættet benytter man i matematik statiske deskriptorer. Vi introducerer de deskriptorer, man skal kunne i gymnasiet.
Observationssættets størrelse
Observationssættets størrelse er det samlede observationer. I vores tabel ovenfor er observationssættet 13, da vi observerer de 13 drenges højder.
Typetal
Typetal er den observation, i vores tilfælde højde, der har den største hyppighed. I vores tilfælde eksisterer der 2 typetal, nemlig 179 samt 186. Da disse observationer forekommer 2 gange og alle andre en enkelt gang.
Middelværdi
Middelværdien kaldes også for middeltallet samt gennemsnittet. Den beregnes ved at lægge alle observationer sammen og herefter dividere med antallet af observationer.
Middelværdien kan vi i vores tilfælde beregne til 180
Fraktiler og Box plot
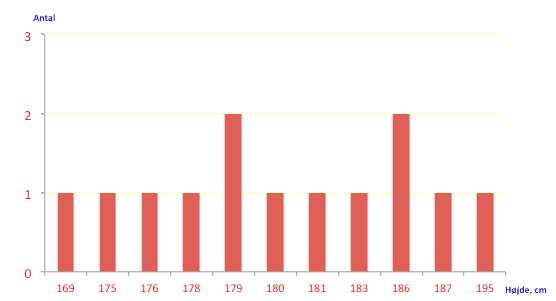
For at få et visuelt overblik illustrerer man ofte observationssættet i diagrammer. Vi har her lavet en stolpediagram over højdefordelingen i klassen. Vi kan faktisk give et endnu bedre visuelt overblik over højde fordelingen ved anvendelse af et såkaldt box plot.
Box plot
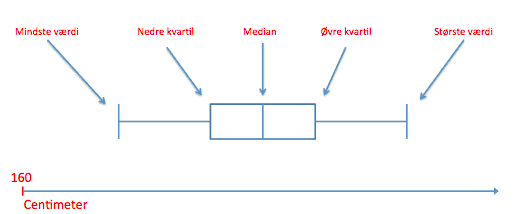
Vi ser herunder en box plot, også kaldet for kassediagram. Box plots giver læseren et hurtigt overblik over en fordeling. I dette eksempel altså fordelingen over højden.
De lodrette linjer i selve “kroppen” i diagrammet angiver nedre kvartil, medianen og øvre kvartil. Nedre kvartil er også kaldt for 1. kvartil og angiver de nederste 25% af observationerne. Medianen angiver den midterste observation. Hvis der er et ulige antal observationer angiver medianen gennemsnittet af de 2 midterste observationer. Øvre kvartil også kaldet for 3. kvartil og angiver således de nederste 75% af observationerne.
.