Vi har i den tidligere lektion defineret følgende statistiske deskriptorer: observationssættet, typetallet samt middelværdien.
Vi går her et skridt videre og introducerer flere statistiske deskriptorer. Vi så tidligere at middeltallet er defineret som:
\(\bar{x}=\frac{x_1+x_2+x_3+\ldots+x_n}{n}\)
I matematik kan vi faktisk skrive formlen for middeltallet på en mere kompakt måde.
\(\bar{x}=\frac{x_1+x_2+x_3+\ldots+x_n}{n}=\frac{\sum_{i=1}^nx_i}{n}\)
På højresiden af sidste lighedstegn, har vi anvendt summationstegnet. Det græske bogstav bruges ofte til at angive, at tal skal lægges sammen. Bogstavet \(i\) er en variabel, som løber fra 1 til \(n\). Udover at beregne middeltallet har man ofte behov for at beregne, hvordan de observerede værdier spreder sig omkring middelværdien. Vi vil her introducere vores næste statiske deskriptorer.
Varians og standardafvigelse
\(\sigma^2(x)=\frac{\sum_{i=1}^n(x_1-\bar{x})^2}{n}\)
Vi ser her definitionen for variansen. Variansen er et tal, der angiver spredningen af observationerne omkring middeltallet, jo større variansen er, des større er spredningen omkring middeltallet.
\(\sqrt{\sigma^2(x)}=\sqrt{\frac{\sum_{i=1}^n(x_i-\bar{x})^2}{n}}\)
\(\sigma(x)=\frac{\sum_{i=1}^n (x_i-\bar{x})}{n}\)
Vi ser her standardafvigelsen for et observationssæt/datasæt. Standardafvigelsen er blot kvadratroden af variansen og angiver således også variationen omkring middeltallet. Jo større standardafvigelse, des større er spredningen omkring middeltallet.
Eksempel
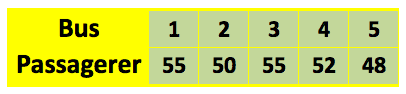
Lad os her lave en foreløbig opsamling med et eksempel. Antag her at en landsby besidder 5 bybusser og byen skal til at føre statistik over antallet af buspassagerer i løbet af en mandag. Landsbyen har noteret følgende observationer
Vi ser nu, hvorledes man bestemmer typetallet, middelværdien, varians samt standardafvigelse med udgangspunkt i datasættet