Polynomiumsdivision

I dette kapital skal vi se, hvorledes vi kan dividere et fleregradspolynomium og den vej, bestemme dens rødder. Du kan vel godt huske fra folkeskolen, hvorledes man dividere et tal med et andet tal.

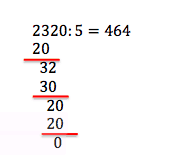
Vi ser altså her, at 5 går 464 gange op i 2320. På samme vis kan vi også dividere polynomier med en flerleddet størrelse. Grunden til at vi overhovedet vil bruge tid på at dividere et polynomium med en størrelse er at vi på denne måde kan omskrive “pæne” fleregradspolynomier til produktet af 2 eller flere størrelser og på denne måde er det nemmere at se, hvilke x-værdier der resulterer i at fleregradspolynomiet bliver lig 0 og vi dermed har bestemt rødderne.

Vi skal her se, hvorledes vi udfører en polynomiums division.

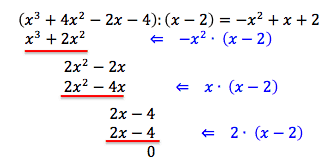
Vi ser her et eksempel på, hvorledes vi kan dividere et trejdegradspolynomium med et 2 ledet størrelse. Vi kan altså her konkludere, at vi kan omskrive trejdegradspolynomiet til produktet af:

\((x^3+4x^2-2x-4)=(x-2)\cdot(-x^2+x+2)\)

Husk at grunden til at vi dividerer et fleregradspolynomium, er jo at simplificere polynomiet, dvs. gør det simplere at overskue med det formål at bestemme rødderne. For at bestemme rødderne skal vi altså sætte polynomiet lig 0 og finde (beregne) de tal, sat ind på \(x\)’ernes plads, i polynomiet således at polynomiet giver 0. Hvis eksempelvis ovennævnte trejdegradsligning er forskriften for et polynomium, bestemmer vi dens rødder ved at løse ligningen

\(f(x)=x^3+4x^2-2x-4 \rightarrow f(x)=0 \leftrightarrow\)

\(x^3+4x^2-2x-4=0\)

og vi ved polynomiums division kan vi altså omskrive trejdegradspolynomiet til et mere simpelt udtryk. Det er ret nemt at se en af løsningerne her, nemlig \(x=2\).

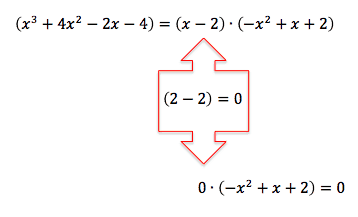
Den ene løsning er altså 0, den anden løsningen finder vi ved at finde det tal, sat ind på x’ernes plads i andengradsligningen i parentesen der resulterer i et nul. Dvs., vi løser nu ligningen:

\((-x^2+x+2)=0\leftrightarrow \frac{-1\pm\sqrt{1^2-4\cdot(-1)\cdot 2}}{2\cdot(-1)} \leftrightarrow x=\{-1, 2\}\)

Hermed har vi nu bestemt løsningsmængden. Løsningen er altså \(x=-1\) og \(x=2\).

Opgave                                                                                                                                              

Udregn nulpunkter for følgende trejdegradspolynomium

\(f(x)=x^3+2x^2-10x-20\)

ved at dividere polynomiet med \((x+2)\)

Løsning