Vi har tidligere afsnit set, at en ret linje kan fastlægges ved et kendt punkt og den tilhørende normalvektor. I dette afsnit vil vi fastlægge en plan, ved hjælp af et punkt og en normalvektor.
\(P_0=(x_0,y_0,z_0),\quad P=(x, y,z),\quad\vec{n}=\left(\begin{matrix} a \\ b \\ c \end{matrix}\right)\)
Der gælder nu ligesom i den todimensionale verden, at planen udgør mængden af alle de punkter \(P(x,y,z)\), der opfylder at:
\(\vec{P_0P}\cdot\vec{n}=0\leftrightarrow\left(\begin{matrix} x-x_0 \\ y-y_0 \\ z-z_0 \end{matrix}\right)\cdot\left(\begin{matrix} a \\ b \\ c \end{matrix}\right)=0\)
Udregner vi herefter skalaproduktet fremkommer planens ligning:
\(a(x-x_0)+b(y-y_0)+c(z-z_0)=0\)
Læg mærke til her at i forhold til det todimensionale rum, er her kommet et led mere på. Lad os her kigge på et konkret eksempel, hvor vi givet et punkt samt en normalvektor beregner planens ligning.
Der er her givet 1 punkt \(P_0=(1,2,3)\) og en normalvektor \(\vec{n}=\left(\begin{matrix} 1 \\ 3 \\ 2 \end{matrix}\right)\). Vi kan nu beregne prikproduktet:
\(\vec{P_0P}\cdot\vec{n}=0\leftrightarrow 1(x-1)+3(y-2)+2(z-3)=0\)
Planens ligning bliver
\(x-1+3y-6+2z-6=0\leftrightarrow x+3y+2z=13\)
Parameterfremstilling for en plan
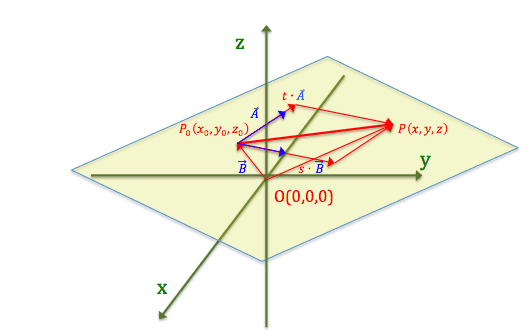
Har man en vektor, der ligger i en plan, har man med en retningsvektorer at gøre. Det vil sige en retningsvektor for planen. Har vi 2 retningsvektorer der ikke er parallelle og et kendt punkt, kan man opskrive en parameterfremstilling for planen.
Vi har her på tegningen indtegnet det kendte punkt og 2 retningsvektorer. Læg her mærke til
\(\vec{P_0P}=s\vec{B}+t\vec{A}\)
Lader vi \(s\) og \(t\) løbe gennem alle mulige tal, vil vores “løbende punkt” \(P\) gennemløbe alle punkter i planen. Vi kan også bestemme stedvektoren til \(P\) ved hjælp af indskudsreglen:
\(\vec{OP}=\vec{OP_0}+\vec{P_0P}\)
\(\vec{OP}=\vec{OP_0}+s\vec{B}+t\vec{A}\)
Vi har nu fundet frem til planens parameterfremstilling
\(\left(\begin{matrix} x \\ y \\ z \end{matrix}\right)=\left(\begin{matrix} x_0 \\ y_0 \\ z_0 \end{matrix}\right)+s\cdot\left(\begin{matrix} b_1 \\ b_2 \\ b_3 \end{matrix}\right)+t\cdot\left(\begin{matrix} a_1 \\ a_2 \\ a_3 \end{matrix}\right)\)
Afstand fra punkt til plan
Vi vil her præsentere formlen for afstanden fra et punkt til en plan. Afstanden fra et punkt \(P_0(x_0,y_0,z_0)\) til en plan \(\alpha\) med følgende ligning
\(ax+by+cz+d=0\)
Kan beregnes ved følgende formel
\(dist(P_0, \alpha)=\frac{|ax_0+by_0+cz_0+d|}{\sqrt{a^2+b^2+c^2}}\)
dist står for det engelske ord distance, på dansk afstand. Beviset for formlen minder om den tilsvarende formel for afstanden mellem et punkt til en linje i to dimensioner.
Vinkel mellem linje og plan
I visse tilfælde er man interesseret i at beregne vinklen \(v\) mellem en linje og en plan. For at beregne vinklen skal man først starte med at beregne vinklen \(u\) mellem en normalvektor for planen og retningsvektoren for linjen ud fra skæringspunktet. Herefter kan vinklen \(v\) bestemmes. Vinklen \(u\) mellem normalvektoren, \(\vec{n}\), og retningsvektoren, \(\vec{r}\), for linjen ud fra skæringspunktet kan bestemmes ved følgende formel:
\(\cos{(u)}=\frac{\vec{r}\cdot\vec{n}}{|\vec{r}|\cdot|\vec{n}|}\)
Vinklen \(v\) mellem linjen af planen finder man som \(v=u-90°\).
Lad os herefter kigge på et konkret eksempel, hvor ovenstående formel anvendes.
Vi antager, at vi har fået givet en linje med følgende parameterfremstilling:
\(l: \left(\begin{matrix} x \\ y \\ z \end{matrix}\right)=\left(\begin{matrix} 1 \\ 3 \\ 4 \end{matrix}\right)+t\cdot\left(\begin{matrix} 2 \\ -1 \\ 3 \end{matrix}\right)\)
Der antages yderligere, at linjen danner en vinkel \(v\) med \(y-z\) planen. Denne vinkel vil vi beregne. Vi starter først med at beregne vinklen mellem retningsvektoren for linjen samt normalvektoren for planen, der i dette tilfælde har ligningen \(x=0\).
\(\cos{(u)}=\frac{\vec{r}\cdot\vec{n}}{|\vec{r}|\cdot|\vec{n}|}=\frac{2}{\sqrt{14}\cdot 1}≈0,53\rightarrow u≈57,7°\)
Vinklen \(v\) bliver derfor \(v=90°-u≈32,3°\).
Vinkel mellem to planer
Har man to planer, der skærer hinanden i en linje \(I\). Da kan man bestemme vinklen mellem disse 2 planer ved at beregne vinklen mellem disse 2 planers normalvektorer afsat på linjen \(I\). Denne vinkel bestemmes af:
\(\cos{(v)}=\frac{\vec{n}_\alpha\cdot\vec{n}_\beta}{|\vec{n}_\alpha|\cdot|\vec{n}_\beta|}\)
Lad os tage udgangspunkt i et konkret eksempel. Vi ønsker her at beregne vinklen mellem 2 planer.
Der er givet to planer
\(\alpha: x-1y+3z-6=0\quad\quad\beta: x-4y-8=0\)
De to vektorer er:
\(\vec{n}_\alpha=\left(\begin{matrix} 1 \\ -1 \\ 3 \end{matrix}\right),\quad\quad\vec{n}_\beta=\left(\begin{matrix} 1 \\ -4 \\ 0 \end{matrix}\right)\)
Vinklen mellem de 2 planer beregnes ved:
\(\cos{(v)}=\frac{\left(\begin{matrix} 1 \\ -1 \\ 3 \end{matrix}\right)\cdot\left(\begin{matrix} 1 \\ -4 \\ 0 \end{matrix}\right)}{\sqrt{11}\cdot\sqrt{17}}≈0,3241\)
Dvs. \(v=\cos^{-1}(0,3241)=71,08°\).
Opgaver
Bestem planens ligning, givet et kendt punkt samt en normalvektor:
\(a(x-x_0)+b(y-y_0)+c(z-z_0)=0\)
- \(P_0(2,1,4)\quad\quad\,\,\,\,\, N=\left(\begin{matrix} 2 \\ 2 \\ 3 \end{matrix}\right)\)
- \(P_0(1,-2,2)\quad\quad N=\left(\begin{matrix} 1 \\ -1 \\ 2 \end{matrix}\right)\)
Se løsning
Der er givet 3 punkter:
\(A(6,0,0)\)
\(B(0,8,0)\)
\(C(0,0,10)\)
- Bestem parameterfremstillingen for planen ABC
- Undersøg om punktet \(P\) ligger i planen: \(P=(3,4,8)\)
Se løsningen