I denne sektion vil vi kigge lidt nærmere på sammenhængen mellem, når en differentiabel funktion \(f(x)\) vokser/aftager og fortegnet for dens afledede funktion \(f'(x)\). Det viser sig nemlig, at der er en klar sammenhæng mellem en funktions monotoniforhold og dens afledede funktions fortegn. Med andre ord, så kan vi altså anvende fortegnet for den afledede til at bestemme funktionens såkaldte monotoniforhold.
En funktions monotoniinterval viser, i hvilket interval på x-aksen funktionen \(f(x)\) enten er voksende/aftagende.
Maksimum, minimum samt vendetangenter
I nogle tilfælde støder man ind på funktioner \(f(x)\), hvor de enten er voksende overalt eller aftagende overalt undtagen i et enkelt punkt, hvor de hverken er voksende eller aftagende. I disse tilfælde er \(f'(x)\) enten voksende eller aftagende og der, hvor \(f(x)\) hverken vokser eller falder, er \(f'(x)=0\).
Lad os som det næste udføre en eksakt beregning af monotoniforholdene for en parabel og bestemme dens toppunkt ved hjælp af en vendetangent. Vi tager derfor udgangspunkt i følgende forskrift
\(f(x)=x^2-8x+15\)
Fremgangsmåden kan stilles i 3 simple punkter.
1. Beregn \(f'(x)\)
\(f'(x)=2x-8\)
2. Beregn \(f'(x)=0\)
\(f'(x)=0\)
\(2x-8=0\)
\(x=4\)
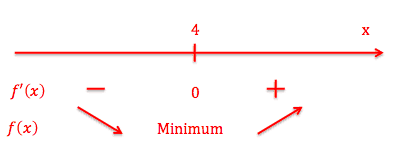
Vi ser altså her, at for en \(x\) værdi på \(4\) er \(f'(x)=0\), dvs. tangenten er vandret. Der gælder, at det eneste punkt på enhver parabel, hvor tangenten kan være vandret, er kun i toppunktet. Her går parablen fra at være voksende til faldende eller omvendt. Vores toppunkt har altså x-koordinaten \(4\).
3. Tegn fortegnslinje
Det ligetil at se, at \(f'(x)>0\) for \(x>4\), og omvendt at \(f'(x)<0\) for \(x<4\). Vi kan altså konkludere at funktionen er voksende for \(x>4\) samt aftagende for \(x<4\).
Vi kan nu opsummere vores iagttagelser i en såkaldt monotonilinje. Monotonilinjen angiver monotoniforholdene for funktionen \(f(x)\).
De skrå røde pile angiver, at \(f(x)\) er positiv, og at \(f(x)\) aftager, når og kun når \(f'(x)\) er negativ. Og den vokser altså, når og kun når \(f'(x)\) er positiv. Lad os gå videre med endnu et eksempel.

Vi skal her se, hvorledes man kan gennemføre en præcis beregning af en af ovenstående funktions monotoniforhold. Vi undersøger følgende funktion:
\(f(x)=2x^3+3\)
Fremgangsmåden kan stilles i 3 simple punkter.
1. Beregn \(f'(x)\)
\(f'(x)=6x^2\)
2. Beregn \(f'(x)=0\)
\(f'(x)=0\)
\(6x^2=0\)
\(x=0\)
3. Tegn fortegnslinje
Nulpunktet for \(f'(x)\) deler x-aksen i 2 intervaller. Vi skal nu for hvert interval undersøge, hvorvidt \(f'(x)\) er negativ eller positiv. Dette gøres ved at beregne en værdi af \(f'(x)\) i hvert interval.
\(f'(-1)=6\)
\(f'(1)=6\)
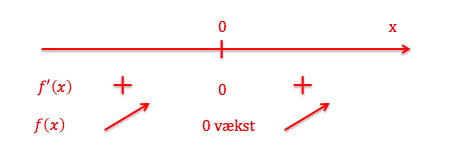
Med følgende viden kan vi nu tegne en oversigt over monotoniforholdene for funktionen f.
De skrå pile vi ser, angiver at \(f\) vokser.
Opgave
Vi har følgende funktion:
\(f(x)=x^3\cdot\ln{(x)}\)
a) Forklar præcis, hvad der sker på de 4 nedenstående linjer:
\(f'(x)=3x^2\cdot\ln{(x)}+x^3\cdot\frac{1}{x}\)
\(0=(3\ln{(x)}+1)x^2\)
\(-1=3\ln{(x)}\)
\(e^{\frac{-1}{3}}=x\)
b) Bestem monotoniforholdene for funktionen \(f\).
Løsning