Visse ligninger er nemme at løse. De fleste kan løse ligningen \(x+1=2\). De fleste vil ret hurtigt kunne se, at hvis vi indsætter 1 på \(x\)’s plads vil ligningen stemme. Indsættes alle andre tal ind på \(x\)’s plads vil ligningen vil der derimod ikke stemme. Ligningen har derfor løsningen \(x=1\).
I denne sektion skal vi se, hvorledes man løser ligninger. Der er flere måder hvorpå man kan løse ligninger, blandt andet ved grafiske metoder, grafregner EXCEL og naturligvis blyant og papir.
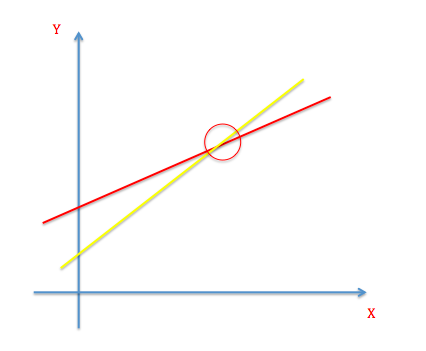
Figuren viser graferne for 2 funktioner, der beskriver en vilkårlig udvikling. Det interessante i dette tilfælde er skæringspunktet mellem den gule og røde graf. Vi ser at op til skæringspunktet, da har den røde graf højere \(y\)-værdier. I skæringspunktet besidder de begge samme \(y\)-værdi, og efter skæringspunktet har den gule rette linje højere \(y\)-værdier.
Vi kan her stille spørgsmålet: “Hvornår har de 2 funktioner lige store funktionsværdier?”. Svaret er, at det er de, hvor de 2 grafer skærer hinanden. Her har de præcis samme funktionsværdi.
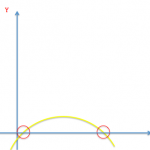
Ovenstående figur viser grafen for en funktion, \(f\). De 2 skæringspunkter med \(x\)-aksen kaldes funktionens nulpunkter. Da \(y=0\) for alle punkter på \(x\)-aksen, må nulpunkternes \(x\)-koordinater være løsningerne til \(f(x)=0\).
To forskrifter
Skal man løse en ligning af typen \(f(x)=g(x)\), hvor både \(f\) og \(g\) har kendte forskrifter, har man flere muligheder. Man kan ligesom i den første figur vælge at tegne de 2 grafer i et koordinatsystem og aflæse skæringspunkterne. Man kan dog også løse ligningen ved formelregning. Det handler om at samle alle \(x\)’erne på den ene side af lighedstegnet og alle konstanter (tal) på den anden side.
\(f(x)=2x+12,\quad g(x)=3x-3\)
\(f(x)=g(x)\)
\(2x+12=3x-3\)
\(2x+12-2x=3x-3-2x\)
\(12=x-3\)
\(12+3=x-3+3\)
\(x=15\)
I dette tilfælde ser vi at løsningen til ligningen er \(x=15\). Sætter vi eksempelvis 15 ind på \(x\)’ernes plads i de 2 ligninger gå de op. Et andet eksempel:
\(f(x)=-2x+4,\quad g(x)=x-6\)
\(f(x)=g(x)\)
\(-2x+4=x-6\)
\(-2x+2x+4=x-6+2x\)
\(4=3x-6\)
\(4+6=3x-6+6\)
\(10=3x\)
\(x=\frac{10}{3}\)
Vi ser endnu et eksempel, hvor vi løser en ligning ved hjælp af elementære regneregler. Løsningen i dette tilfælde er \(x=\frac{10}{3}\). For at løse ligninger, skal vi gøre brug af elementære regneregler.
Der gælder at:
- Vi kan dividere på den ene side af lighedstegnet, så længe vi også dividerer den anden side.
- Vi kan lægge til eller trække fra, hvis vi gør det på begge sider af lighedstegnet.
- Vi kan gange på den ene side af lighedstegnet, så længe vi også ganger på den anden side.
Opgaver
Udregn følgende opgaver ved hjælp af blyant og papir.
- \(5x+3=7x-2\)
- \(-(2-5)+7x=2x(2-5)+3\)
- \(12x+x(2-4)=0\)
Se løsningerne
Bestem koordinatsættet til skæringspunkterne ved hjælp af blyant og papir mellem følgende funktioner:
- \(y=5+x\) og \(y=30-\frac{1}{2}x\)
- \(y=14+\frac{1}{2}x\) og \(y=32-\frac{1}{2}x\)
Se løsningerne