En hypotese er en formodning om, at en påstand gælder. Det kan være at “drenge er højere end piger”, eller “piger er bedre til matematik end drenge”. Andre eksempler kan jo være at “piger har større eksamensangst end drenge”, “eksamensangst har en indflydelse på præstationen under matematikeksamenen” eller at “cykling forbrænder flere kalorier end løb”.
Man forsøger ud fra et datasæt(stikprøve) at afgøre, om en given hypotese kan accepteres eller forkastes. Man kan ofte ud fra en veludført stikprøve beregne sandsynligheden for, at hypotesen er rigtig. I tilfælde af, at denne sandsynlighed er høj nok, da accepterer man hypotesen og hvis sandsynligheden er lav, da forkaster man den.
Når man skal udføre en hypotesetest, starter man altså med at udtage stikprøver for at udføre en test. Målet med stikprøven er at understøtte ens hypotese/påstand, medmindre observationerne på en afgørende måde taler imod den. I dette tilfælde forkaster man hypotesen. En hypotese kaldes nulhypotese, når man tager udgangspunkt i en påstand.
Vi kan eksempelvis have nulhypotesen ovenfor “piger er bedre til matematik end drenge”. For at udføre en hypotesetest, kan matematiklæren udfærdige en svær matematikprøve. Prøven uddeles herefter til 100 drenge og 100 piger på skolen. Herefter er tanken at det køn, der har flest rigtige svar må være dygtigst til matematik. Nulhypotesen vil her være at piger og drenge er lige dygtige, i forhold til vores test, vil vi derfor gennemsnitligt forvente samme antal rigtige svar for hvert køn. Modhypotesen vil være, at piger har gennemsnitligt flere rigtige svar end drenge. Fra stikprøven kan man herefter beregne sandsynligheden for, at nulhypotesen er rigtig. Hvis sandsynligheden eksempelvis er på 90 %, accepterer man normalt nulhypotensen. I tilfælde af at sandsynligheden kun er 6 %, da vil matematiklæren forkaste nulhpotesen. Man vil altså forkaste en nulhypotese, hvis den er usandsynlig.
I de fleste tilfælde vælges et signifikansniveau på 5 % og 10 %. Det betyder at man forkaster en nulhypotese, hvis dens sandsynlighed er under henholdsvis 5 % og 10 %. I visse tilfælde anvendes også et signifikansniveau på under 5 %.
T-test for middelværdi
Indenfor hypotesetest, testes for middelværdi i stikprøven til at afgøre om denne middelværdi, stemmer overens med en opgivet værdi. I tilfælde af at spredningen ikke er kendt, anvendes t-test. lad os tage udgangspunkt i nulhypotesen “eleverne fra Vejle kommune scorer højere karakter i spanskundervisning end landsgennemsnittet”. I tilfældet her vil den opgivne værdi være karaktergennemsnittet for spanskeksamenen på landsplan og vi vil derfor teste om karaktergennemsnittet for Vejle kommune i spansk vil være lig med landsgennemsnittet (nulhypotese).
\(\mu=\text{karaktergennemsnit i spansk på landsplan}\)
\(\mu_0=\text{karaktergennemsnit i spansk i Vejle kommune}\)
\(H_0: \mu=\mu_0\)
Eller om modhypotesen holder dvs. elever i Vejle kommune får højere karakterer i spansk end på landsplan.
\(H_1: \mu<\mu_0\)
Om vi accepterer nulhypotesen og konkluderer, at eleverne i Vejle kommune er på samme niveau som alle andre elever i landet afhænger af vores signifikansniveau samt om stikprøven foretaget i Vejle kommune ligger indenfor dette signifikansniveau.
T-test til sammenligning af 2 middelværdier
Man benytter denne slags test, når man vil undersøge om 2 datasæt har samme middelværdi. Vi antager her, at vi vil undersøge om drengene og pigerne i 1.g er lige gode til faget matematik. Matematiklæren uddeler derfor en tidligere eksamensopgave i matematik og herefter giver matematiklæren opgavebesvarelserne et antal point, fra 0 til 100. Resultaterne for drengene ses her:
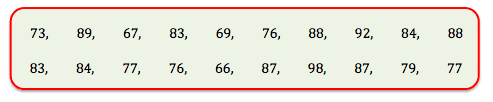
og resultaterne for pigerne har vi lige her
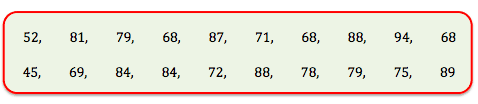
Vi ønsker nu at teste om disse to grupper af elever opnår det samme resultat. Da vi sammenligner middelværdierne, det vil sige gennemsnittet for deres resultater starter vi naturligvis med at beregne middelværdien af de 2 grupper ved anvendelse af følgende formel:
\(\bar{x}=\frac{x_1+x_2+x_3+\ldots+x_n}{n}\)
Her gælder
\(\bar{x}=\mu\)
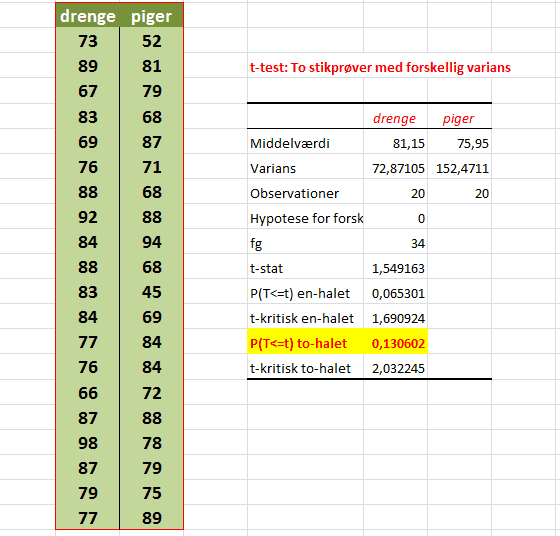
For drengene får vi nu en middelværdi på 81,15 points og for pigerne får vi 75,95 points. Vi ser nu at gennemsnitlig er drengene bedre end pigerne til matematik, men spørgsmålet er om denne forskel er signifikant?
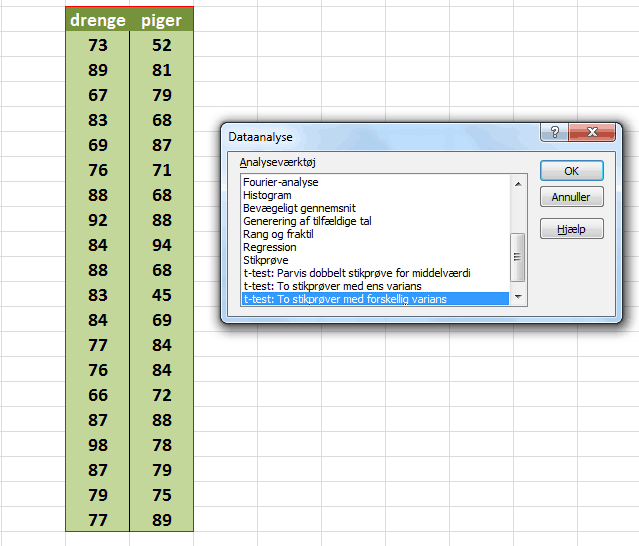
Udregningerne er ret omfattende. Derfor vil vi her anvende EXCEL til at udføre beregningerne for os. Vi vælger EXCELS “dataanalyse” og herefter vælges “t-test: To stikprøver med forskellig varians”
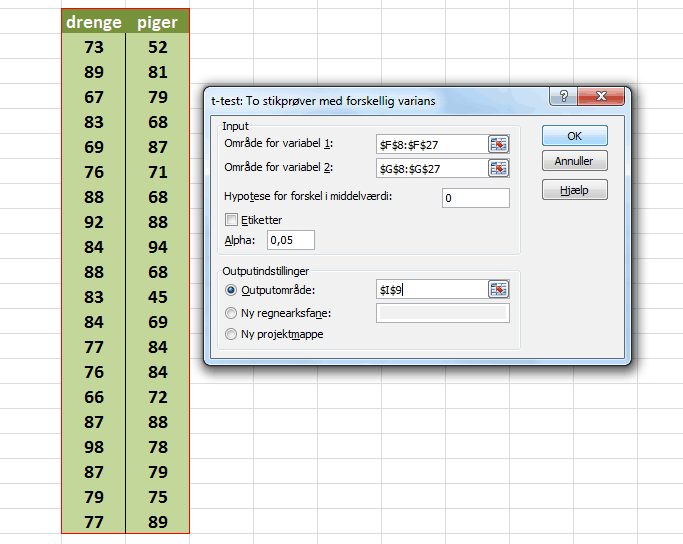
Herefter markerer vi kolonnen “drenge” som “Område for variabel 1”, kolonnen “piger” som “Område for variabel 2”, “Hypotese for forskel i middelværdi” sættes 0 og endelig så vælges en outputområde.
Herefter beregner EXCEL vores sandsynlighed ud. Det ses her at vi får en p-værdi på 0,1306, hvilket fortæller os, at sandsynligheden for, at nulhypotesen er rigtig, er ca. 13 %. Da det altså er over vores sædvanlige signifikansniveau på 5 %, forkaster vi ikke vores nul hypotese om at de 2 grupper er lige gode til matematik.
Selvom vi altså ser, at der er en forskel i gennemsnittet for de 2 grupperinger, er forskellen altså ikke stor nok til at man kan drage en konklusion om at drenge er generelt stærkere til matematik.