I denne sektion skal vi præsentere vektorer. Vektorregning fylder meget i videregående matematik indenfor mange områder. Eksempelvis, hvis du ser vejrudsigten anvendes nogle gange pile, for at illustrere vindens retning samt hastighed. Samme principper gør sig gældende, når vi har med vektorer at gøre.
En vektor er karakteriseret ved, at den har en bestemt retning og en bestemt længde.
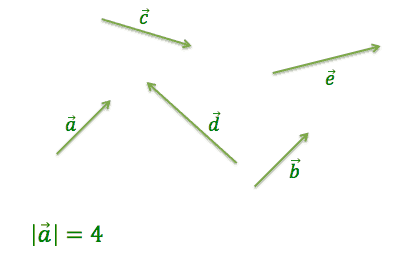
Vi ser her en række vektorer med forskellige længder samt retninger. Som det ses her, så navngives vektorer med bogstaver, herudover sættes typisk en pil el. lignende for at angive at vi har med vektorer at gøre. Vi ser yderligere at vektoren \(a\) har længden 4.
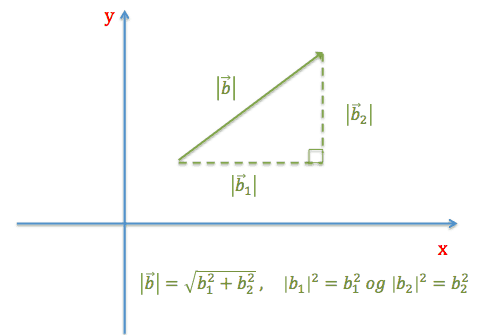
Nedenfor i koordinatsystemet ser vi en vektor. Dens vektors længde kan man beregne ved hjælp af Pythagoras sætning, da kateterne i den retvinklede trekant er kendt, når man får opgivet vektorens koordinatsæt.
Man indsætter vektorer i et koordinatsystem, koordinaterne til det specifikke punkt som pilespidsen ender på, fastlægger både retningen samt længden for vektoren.
Vi ser altså her, at vores vektor har koordinaterne \((5,4)\).Det vil sige, at vektoren bevæger sig 5 enheder på \(x\)–aksen og 4 enheder på \(y\)-aksen.
Her ser vi en anden vektor. Med udgangspunkt i vektorens koordinater ser vi, at \(x\)-koordinaten er -5 og \(y\)-koordinaten er -4, dvs. vektoren går 5 enheder tilbage på \(x\)-aksen og falder med 4 ender på \(y\)-aksen.

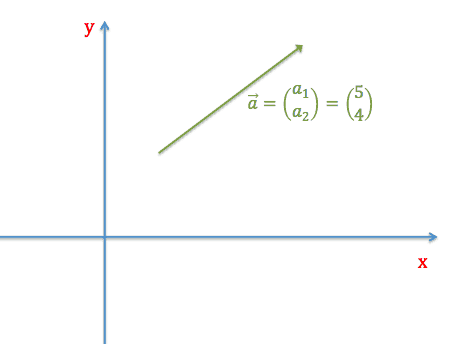
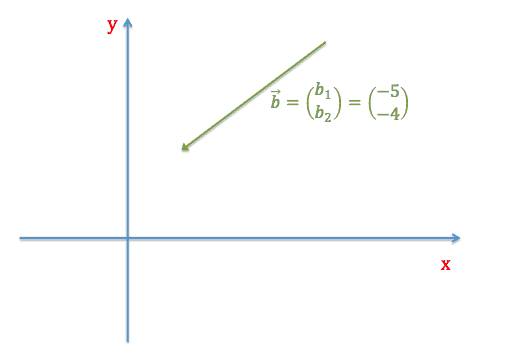












hvad bruger man vektorer til?