I matematik er differentialregning en meget vigtig disciplin. Differentialregning er en ret omfattende matematisk struktur, der kan stille visse krav til abstrakt tænkning. Differentialregning bliver brugt i googles søgefunktioner, indenfor økonomisk modellering, forudsigelse af vejret, mange emner indenfor fysik. Differentialregning i matematik går kort og godt ud på at beregne, hvor hurtigt funktioner aftager/vokser i et bestemt punkt. Matematisk set, så ønsker man at beregne hældningen af tangenten i det enkelte punkt.
Man kan herudover i matematik på gymnasieniveau anvende differentialregning i særlig funktionsanalyse. Vi skal lære differentialregning blandt andet fordi bruge det til at bestemme funktioners minimums og maksimumspunkter, funktioners monotoniforhold, optimering af funktioner og meget andet.
Inden du går videre, vil vi lige her starte med at omtale nogle grundbegreber.
Grænseværdi
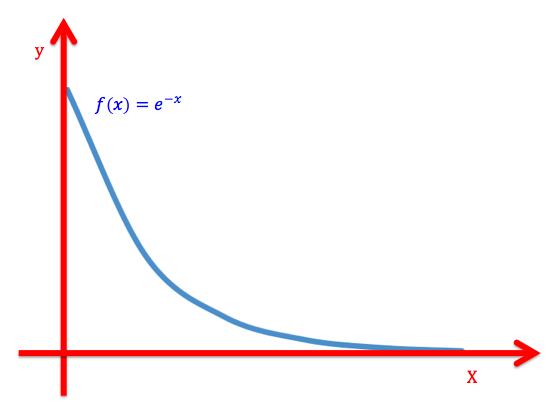
Tager vi udgangspunkt i en eksponentialfunktion
Ser vi at funktionen ikke vil få negative funktionsværdier, eller en funktionsværdi på 0. Den vil med tiden få en funktionsværdi meget tæt på 0, eksempelvis 0,0000000000001, men altså aldrig 0.
I dette tilfælde siger man at funktionen \(f(x)\) har en grænseværdien 0 for \(x\) gående mod uendelig, og skriver det således:
\(f(x)\rightarrow 0\text{ for } x\rightarrow\infty\text{ eller }\lim_{x\rightarrow\infty}f(x)=0\)
Kontinuitet
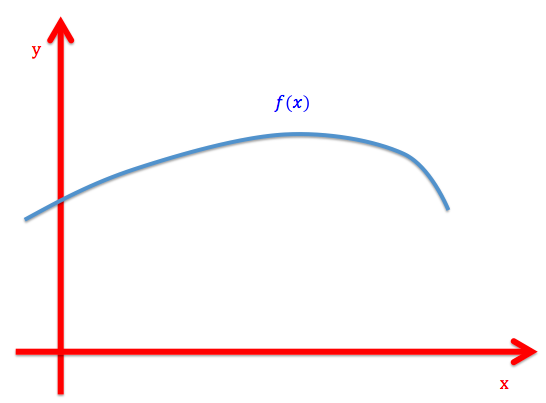
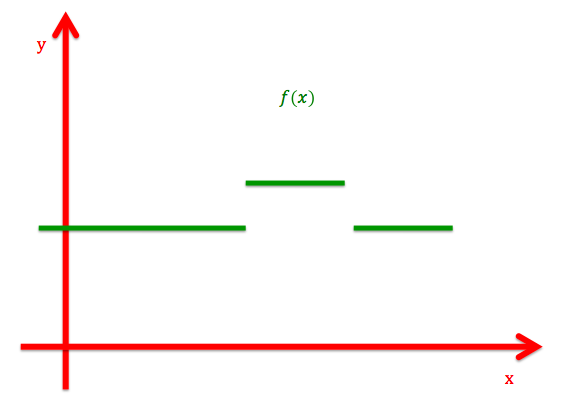
En funktion kaldes kontinuert, hvis dens graf er fuldkommen sammenhængende. Det vil sige at en funktion er kontinuert i et bestemt interval \(a\) til \(b\), hvis man kan tegne grafen i intervallet uden overhovedet at løfte blyanten fra papiret.
Vi ser her ovenover, at funktion \(f(x)\) er kontinuerlig. Det vil sige at man kan tegne den, uden at løfte blyanten.
Det er også ret tydeligt her, at \(f(x)\) ikke er kontinuerlig. Da man skal løfte blyanten for at tegne funktionen. En funktion siges altså at være kontinuert i et interval, hvis den er kontinuert i ethvert punkt i intervallet.