Frekvens og kumuleret frekvens

Lad os her antage at i 1. g har eleverne netop fået årskarakterer i matematik. I klassen er der 2 elever der har fået 00 i matematik, dette behøver dog ikke være ensbetydende med at klassen er super elendig til matematik. Hvis der kun er 2 ud af 30 elever der har fået 00 i matematik, kunne det måske godt tænkes at klassen er god nok alligevel.

Frekvens

Den procent, en bestemt observations hyppighed udgør af hele observationssættets samlede størrelse, kaldes for frekvens.

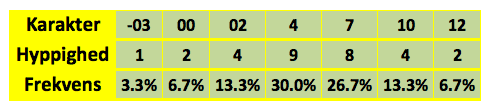
Vi ser her karakterfordelingen for 1. g. Vi ser eksempelvis her, at 2 elever har fået 12 i matematik. Lægger vi hyppighederne sammen, får vi 30. Dette er observationssættets størrelse. Frekvensen i procent kan generelt defineret som

\(\text{frekvens}=\frac{\text{hyppighed}}{\text{observationssættes størrelse}}\cdot 100\)

Frekvensen angiver således i eksemplet ovenfor, at der kun er 6,7% der har har fået karakteren 00. Dette er ikke så slemt igen, end hvis frekvensen af elever der har fået 00 er eksempelvis var på 30%. Så vi kan jo konkludere at klassen ikke er så dårlig igen til matematik.

Kumuleret frekvens

Vi kan dog også beregne, hvor mange elever der har dumpet i matematik. Det vil sige, hvor mange elever der har fået karakteren 00 eller derunder. Fra tabellen kan vi se, at 3,3% af klassen har fået karakteren -03, herudover har 6,7% af klassen fået karakteren 00. Vi ser altså at 10% af eleverne har dumpet (3,3 % + 6,7 % = 10 %). Vi har faktisk her beregnet den såkaldte kumulerede frekvens af observationen 00.

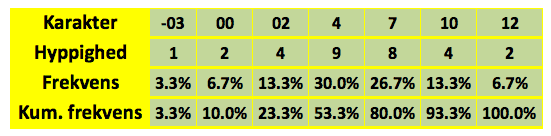
Kumuleret betyder det samme opsummeret og vi kan i tabellen altså se at op til 80 % af klassen har fået op til karakteren 7, eller at 20 % (100 % – 80 %) af klassen har fået over 7 i karakter.

Du kan i animationen nedenunder se, hvorledes man præcis regner både frekvens samt kumuleret frekvens ud og herefter bestemmer kvartilsættet.

Eksempel 

Når man ønsker at illustrere både frekvens samt kumulerede frekvenser ren grafisk, så tegner man henholdsvis et såkaldt pinde- og trappediagram. Herefter kan man også nemt aflæse både kvartilsættet samt fraktiler. Sidstnævnte det vil sige, fraktil betyder det samme som brøkdel. Man definerer generelt \(x\) % fraktilen som den mindste observation i observationssættet, hvis kumulerede frekvens er mindst \(x\) %.  

Se animationen herunder for yderligere detaljer.

Eksempel