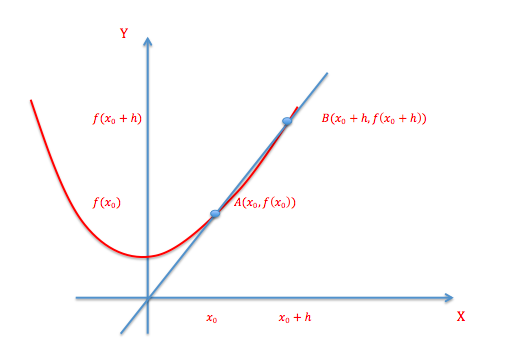
Vi skal her kigge nærmere på differentialkvotienten, derfor strammer skruen en smule og kaster et blik på vores sekant.
Som før begynder vi med at bestemme sekantens hældning, der også kaldes for differenskvotienten, fordi den jo består af en kvotient mellem 2 differencer.
\(a_s=\frac{y_2-y_1}{x_2-x_1}=\frac{f(x_0+h)-f(x_0)}{(x_0+h)-x_0}\)
Vi antager nu at den røde funktion i koordinatsystem foroven har forskriften
\(f(x)=\frac{1}{2}x^2+1\)
Vi ønsker nu at bestemme tangentens hældning (den blå rette linje) i en vilkårlig \(x\)-værdi, som vi kalder for
\(x_0\)
med udgangspunkt i sekantens hældning foroven og definitionen grænsetilfældet for \(\Delta x\) som
\(\Delta x\rightarrow 0\)
Anvender vi nu \(f(x)\) som udgangspunkt for at beregne sekantens hældning i grænsetilfældet får vi:
\(a_s=\frac{\frac{1}{2}(x_0+\Delta x)^2+1-\left(\frac{1}{2}(x_0)^2+1\right)}{\Delta x}\)
\(=\frac{\frac{1}{2}x^2_0+\frac{1}{2}\Delta x^2+\frac{1}{2}2x_0\Delta x+1-\left(\frac{1}{2}(x_0)^2+1\right)}{\Delta x}\)
Vi hæver nu minus parentesen og ser nu, at 2 led i sidste ligning går ud med hinanden.
\(=\frac{\frac{1}{2}x^2_0+\frac{1}{2}\Delta x^2+\frac{1}{2}2x_0\Delta x+1-\frac{1}{2}x_0^2-1}{\Delta x}\)
\(=\frac{\frac{1}{2}\Delta x^2_0+\frac{1}{2}2x_0\Delta x+1-1}{\Delta x}\)
Vi kan nu se at de sidste 2 led går ud med hinanden og vi kan yderligere forkorte med \(\Delta x\) i både tæller og nævner.
\(=\frac{1}{2}\Delta x+x_0\)
Vi har nu bestemt sekantens hældning. I grænsetilfældet får vi tangentens hældning. Det vil sige, når \(\Delta x\) går mod 0. Med andre ord, så finder vi tangentens hældning til:
\(\frac{1}{2}\Delta x+x_0\rightarrow x_0\text{ for }\Delta x\rightarrow 0\)
Mere generelt kan vi skrive differentialkvotienten for \(f(x)\) som
\(f'(x)=x_0\)