Vi har hidtil set på ligninger for rette linjer samt parabler i koordinatsystemer. Vi skal her se, hvorledes man konstruerer cirkler i et koordinatsystem. Ved hjælp af afstandsformlen ønsker vi her i kapitlet at udlede ligningen for en cirkel. Matematisk set, svarer det altså til at bestemme den sammenhæng mellem \(x\) og \(y\), som vil danne et cirkel i et koordinatsystem.
Cirklens ligning
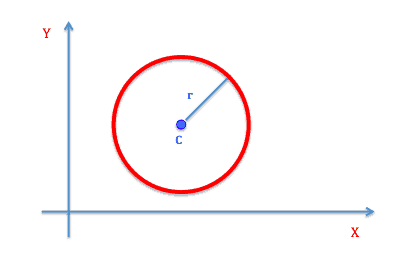
Vi ved alle at en cirkel er pæn og rund. Der gælder at, alle punkter på cirklen har samme afstand til centrum.
Figuren foroven viser en cirkel med radius \(r\) og centrum \(c\). En cirkel med centrum i \(C=(a,b)\) og radius \(r\) har ligningen:
\((x-a)^2+(y-b)^2=r^2\)
Der gælder altså at alle punkter \((x,y)\) der passer ind i cirklens ligning, må ligge på selve cirklen.
Lad os se på et eksempel, vi har her ligningen for en cirkel:
En cirkel med centrum i \(C=(2,3)\) og radius \(5\) har ligningen:
\((x-2)^2+(y-3)^2=25\)
Cirklen har altså centrum i punktet \((2,3)\) og en radius på \(5\). Læg naturligvis mærke til at en cirkel ikke kan have en negativ radius.
Tangent til en cirkel
Vi skal i denne sektion kigge nærmere på cirklens tangent. En tangent til en cirkel er den rette linje, der netop rører cirklen i et enkelt punkt.
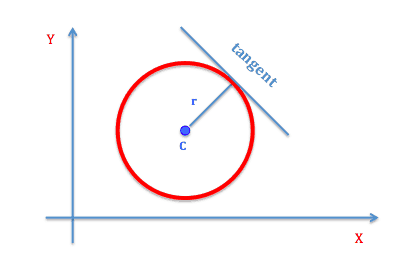
Der gælder faktisk at en cirkels tangent altid vil stå vinkelret på cirklens radius. Vi beviser i videoen forneden, at en cirkeltangent altid vil stå vinkelret på radius i røringspunktet.
Vi skal her se på et eksempel på, hvorledes vi beregner en cirkels tangent. Når vi kender cirklens centrum samt tangentens røringspunkt. Antager vi at en cirkel har centrum i punktet \(C(3,2)\) og yderligere en tangent i punktet \(P(7,5)\). Så kan vi beregne normalvektoren til tangenten i punktet \(P\).
\(\vec{n}=\vec{CP}=\begin{pmatrix} 7-3 \\ 5-2 \end{pmatrix}=\begin{pmatrix} 4 \\ 3 \end{pmatrix}\)
Som et punkt på cirklen anvendes punktet \(P(7,5)\), vi får nu ligningen:
\(4(x-7)+3(y-5)=0\)
\(4x-28+3y-15=0\)
\(4x+3y=43\)
\(y=\frac{43}{3}-\frac{4}{3}x\)
Skæring mellem linje og cirkel
I tilfælde af, at vi ønsker at undersøge om en cirkel samt en linje skærer hinanden, kan man indtegne disse ind i EXCEL og se om de skærer hinanden, hvorefter potentielle skæringspunkters koordinater kan aflæses.
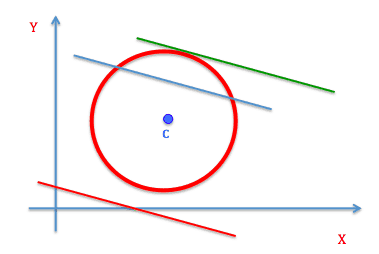
Vi ser i figuren foroven 3 mulige scenarier, enten kan en linje skære cirklen 2 steder (den blå linje). Linjen skærer ét sted (den grønne linje) den sidste mulighed er, at linjen ikke skærer cirklen overhovedet (den røde linje). Mere matematisk kan vi også definere det således:
- Når \(r>d=dist(C,l)\), da skærer linjen cirklen i 2 punkter.
- Når \(r=d=dist(C,l)\), da skærer linjen cirklen i 1 punkt.
- Når \(r<d=dist(C,l)\), da skærer linjen ikke cirklen.
Lad os her se et simpelt eksempel i forhold til punkt 1.
\(y=-x+6\)
\((x-2)^2+(y-3)^2=6\)
Vi indsætter nu \(-x+6\) ind på \(y\)’s plads i cirklens ligning.
\((x-2)^2+(-x+6-3)^2=6\)
\((x-2)^2+(-x+3)^2=6\)
\(x^2+4-4x+x^2+9-6x=6\)
\(2x^2-10x-1=0\)
Vi får her en andengradsligning, hvor diskriminanten er 108 og dermed må have 2 skæringspunkter.
Opgaver
Udregn tangenten i punktet B, på cirklen.
\((x-1)^2+(y-1)^2=25\)
\(B(1,6)\)
Løsning
Opgave
En cirkel er givet ved ligningen:
\((x+4)^2+(y-2)^2=20\)
Vis at punktet \(p(-2,6)\) ligger på cirklen. Bestem en ligning for tangenten i punktet \(p\).
Løsning