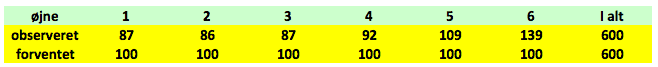Vi skal her gå videre med flere statistiske tests. Der eksisterer et test ved navn chi i anden.
Chi i anden
\(\chi^2 – \text{goodness of fit}\)
Eller også goodness of fit, på engelsk.
Med chi i anden, kan man teste om en række observerede talværdier stemmer overens med tilsvarende forventede værdier. Formlen vi anvender til at teste er som følger:
\(Q=\sum\frac{(\text{observeret-forventet})^2}{\text{forventet}}\)
Formlen er et mål for afvigelsen mellem de observerede og de forventede værdier. Det er dermed indlysende, at jo mindre \(Q\) er, desto bedre er overensstemmelsen mellem de observerede og de forventede værdier.
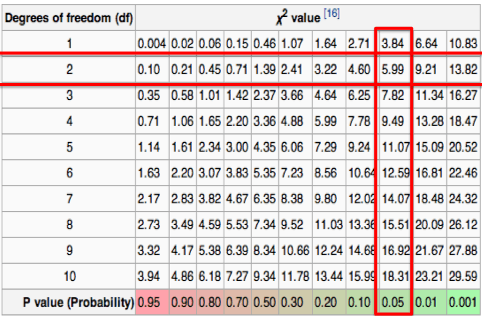
I dag kan man ved hjælp af avancerede lommeregnere samt EXCEL’s funktioner beregne chi i anden tests. I gamle dage slog man op i en tabel for at se, om \(Q\) er høj nok til at man kan forkaste hypotesen. Til mundtlige eksamener skal man helst kunne forklare helt præcist, hvorledes man finder frem til \(Q\)–værdier og hvorledes man skal fortolke resultatet. Derfor skal vi lære den “gamle” metode, det vil sige manuelt beregne os frem til om en given hypotese skal accepteres eller forkastes.
Eksempel
Vi antager her, at en kasinoejer ønsker at udføre en chi i anden test for at undersøge om kasinoets terninger er symmetriske eller om dealerne har udskiftet disse med nogle der ikke er symmetriske til fordel for kunderne. Således at kunne i gennemsnit slår flere 6’er end ellers.
Vores nulhypotese her er, at der er ingen signifikant forskel mellem de observerede samt forventede værdier.
Kasinoejeren kaster med en af terningerne 600 gange og resultatet fremgår i tabellen
Umiddelbart ser det ud som om, at terningen har en tendens til at lande på de høje øjne. Vi beregner først de kvadrerede afvigelser
Herefter dividerer vi nederste række med de forventede værdier
Vi beregner \(Q\) til 22. Spørgsmålet er her om 22 er høj nok en værdi, til at vi kan forkaste vores nulhypotese? For at kunne beregne om \(Q\) er høj nok, skal vi først have beregnet antallet af frihedsgrader, dette beregner man som \(n-1\), da vi har her 6 observationer, dvs. \(n=6\) fås 5 frihedsgrader. Vi slår nu op i en tabel:
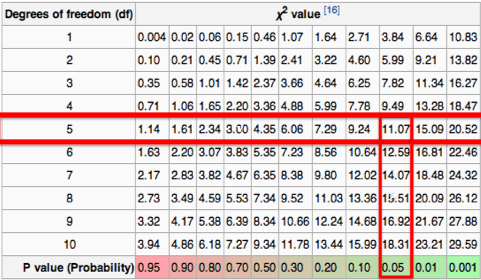
Tabellen her er hentet fra wikipedia, og illustrerer sandsynlighederne for at overensstemmelserne mellem de forventede og observerede værdier. Vi ser her at der er langt under 5 % sandsynlighed for at vi får en \(Q\)-værdi større end 11,07, det vil med andre ord sige, at det er under 5 % sandsynlighed for at de observerede og forventede værdier stemmer overens. Vi har altså her en \(Q\)-værdi på 22, hvilket er meget større end de 11.07, derfor skal vi forkaste nulhypotesen. Det vil sige, at terningerne højst sandsynligt er forfalsket.
Uafhængighedstest
\(\chi^2-\text{Uafhængighedstest}\)
Man kan også teste, om der er uafhængighed mellem rækkerne i en given tabel. Det vil sige, at nulhypotesen vil være at der vil være uafhængighed mellem rækkerne i en tabel eller skema. Dette test kan tænkes anvendt af banker og investeringsselskaber for at undersøge om man eksempelvis forudsige aktiepriser eller prisen på en råvarer ud fra dagens pris. Andre interessante sammenhænge kunne være unges køn og interessen for matematik eller unges køn og eksamensangst og så videre.
Eksempel
Lad os kigge på et eksempel. Vi antager, at vi laver en undersøgelse om interessen for matematik samt køn. Det vil sige, om der er en sammenhæng for matematik samt ens køn. Er drenge mere interesseret i matematik end piger? Eller er det omvendt? Eller er interessen for matematik uafhængig af køn?
Vi antager, at vi laver en undersøgelse i en skole og resultatet ser vi her i skemaet.
Vores nulhypotese er nu, at der er ingen sammenhæng mellem folks køn samt interessen for matematik. Vores nulhypotese siger altså, at de to rækker er uafhængige. Lad os undersøge om dette rent faktisk er tilfældet.
Næste trin er derfor at beregne de forventede værdier baseret på nulhypotesen samt skemaet. Dette gør vi således:

Dette giver følgende forventede værdier

Nu kan vi udføre vores test
\(\chi^2=\frac{(16-21,71)^2}{21,71}+\frac{(238-183,98)^2}{183,98}+\frac{(89-137,31)^2}{137,31}+\frac{(24-18,29)^2}{18,29}\)
\(+\frac{(101-155,02)^2}{155,02}+\frac{(164-115,69)^2}{115,69}=75,13\)
Vi får altså her en \(Q\)-værdi på 75,13. Nu skal vi bestemme frihedsgraderne. Ved uafhængighedstest, gælder der:
Antal frihedsgrader ved uafhængighedstest er givet ved:
\((\text{antal rækker}-1)\cdot(\text{antal søjler}-1)\)
I vores tilfælde har vi altså 2 rækker og 3 søjler, hvilket giver 2 frihedsgrader. Vores kritiske værdi er 5,99, da vores \(Q\)-værdi er på over 75, skal vi forkaste vores nulhypotese. Det vil sige at interessen for matematik i den undersøgte skole er kønsafhængigt.