De fleste personer i Danmark har ofte ikke nok kontanter liggende i skuffen til at kunne købe eksempelvis et hus. Derfor optager de fleste personer et lån i banken for at finansiere købet. Størstedelen af de lån der ydes af banker, finansieringsselskaber og realkreditinstitutter er annuitetslån.
Annuitetslån er karakteriseret ved, at der betales et fast beløb per termin, som kaldes annuitetsydelsen. Annuitetsydelsen dækker både afdraget af selve gælden samt renterne. I starten vil størstedelen af ydelsen tilfalde renteomkostninger. Men over tid vil afdraget udgør en større andel af ydelsen. Selve beløbet der lånes kaldes for hovedstolen.
Vha. af nedenstående formel kan vi beregne annuitetsydelsen:
\(y=A_0\cdot\frac{r}{1-(1+r)^{-n}}\)
Her angiver \(A_0\) hovedstolen (i visse tilfælde bruges bogstavet \(G\) fremfor for \(A\)). Det vil sige det beløb, som lånetageren har lånt. \(r\) står for den terminslige rente. Mens antallet af terminer kaldes for \(n\).
Eksempel
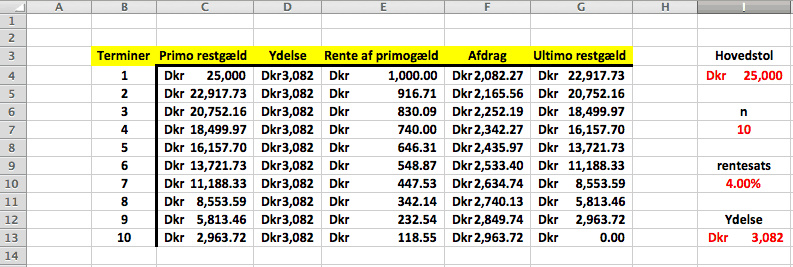
Marie optager et annuitetslån på 25.000 kr. for at finansiere et bilkøb. Hovedstolen inkl. renter skal tilbagebetales over 10 år, hvor vi antager årlige terminer (dvs. \(n=10\)). Vi antager, at den terminslige rentesats er på 4%. Beregn den terminslige ydelse?
Ved at indsætte tallene i formlen for annuitetslån får vi:
\(y=25.000\cdot \frac{0,04}{1-(1+0,04)^{-10}}=3.082\)
Den terminslige ydelse er altså 3.082 kr.
Beregningen kan også foretages i et såkaldt amortisationsskema, oftest i EXCEL, som det ses nedenfor.
For en detaljeret gennemgang og illustration på, hvorledes man laver en fuldkommen amortisationsskema i EXCEL, kan du se følgende video.
Udledning af hovedstolen
Kender vi antallet af terminer, den terminslige ydelse samt renten, kan vi beregne hovedstolen. Det kræver, at vi isolerer hovedstolen, \(A_0\), fra førnævnte formel. Det kan gøres således:
\(y=A_0\cdot\frac{r}{1-(1+r)^{-n}}\)
\(A_0=\frac{y}{\frac{r}{1-(1+r)^{-n}}}\)
\(A_0=\frac{y\cdot (1-(1+r)^{-n})}{r}\)
Udledning af antal terminer
På samme måde kan vi beregne antallet af terminer, hvis vi kender den terminslige ydelse, renten samt hovedstolen. Vi isolerer antallet af terminer således:
\(y=A_0\cdot\frac{r}{1-(1+r)^{-n}}\)
\(1-(1+r)^{-n}=\frac{A_0\cdot r}{y}\)
\((1+r)^{-n}=1-\frac{A_0\cdot r}{y}\)
\(-n\cdot \log{(1+r)}=\log{\left(1-\frac{A_0\cdot r}{y}\right)}\)
\(n=-\frac{\log{\left(1-\frac{A_0\cdot r}{y}\right)}}{\log{(1+r)}}\)
Renteomregning
Renten kan ikke isoleres. Nogen gange er det dog nødvendigt at skulle omregne renten fra f.eks. en årlig rente til en månedlig rente. I det tilfælde skal du bruge nedenstående formel:
\(r_{ny}=(1+r)^{\frac{1}{i}}-1\)
Hvor \(r\) er renten, mens \(i\) er antallet af terminer pr. rentetilskrivning (f.eks. hvis ydelsen er på månedsbasis og vi får oplyst en årlig rente, da er \(i=12\), da der er 12 måneder på ét år).